티스토리 뷰
트리는 계층적 관계를 표현하는 자료구조이다.
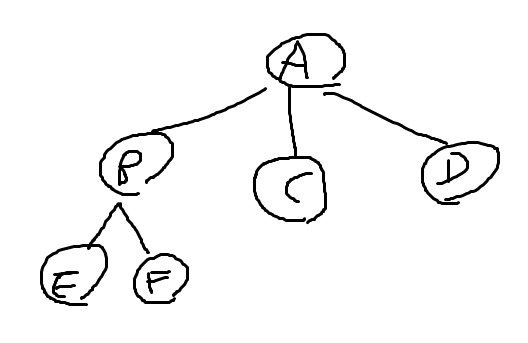
노드(node) : 트리의 구성요소에 해당하는 요소(A, B, C, D)
간선(edge) : 노드와 노드를 연결하는 연결선
루트 노드(root node) : 트리 구조에서 최상위에 존재하는 A와 같은 노드
단말 노드(terminal node) : 아래로 또 다른 노드가 연결되어 있지 않은 노드(E, F)
내부 노드(internal node) : 단말 노드를 제외한 모든 노드
서브 트리 : 큰 트리에 속하는 작은 트리
이진 트리(Binary Tree)
1. 루트 노드를 중심으로 두 개의 서브트리로 나뉘어야 한다.
2. 나뉘어진 두 서브 트리도 모두 이진 트리이어야 한다.
(노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면, 공집합 노드가 존재하는 것으로 간주.
물론 공집합 노드도 이진 트리의 판단에 있어서 노드로 인정)

포화 이진 트리(Full Binary Tree) : 모든 레벨이 꽉 찬 이진 트리
완전 이진 트리(complete binary tree) : 모든 레벨이 꽉 찬 상태는 아니지만, 차곡차곡 빈 틈 없이 노드가 채워진
이진 트리(노드가 위에서 아래로, 왼쪽에서 오른쪽의 순서대로)
ex) 이진트리
BinaryTree.h
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
/*** BTreeNode 관련 연산들 ****/
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endifBinaryTree.c
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));
nd->left = NULL;
nd->right = NULL;
return nd;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
BinaryTreeMain.c
#include <stdio.h>
#include "BinaryTree.h"
int main(void)
{
BTreeNode * bt1 = MakeBTreeNode();
BTreeNode * bt2 = MakeBTreeNode();
BTreeNode * bt3 = MakeBTreeNode();
BTreeNode * bt4 = MakeBTreeNode();
SetData(bt1, 1);
SetData(bt2, 2);
SetData(bt3, 3);
SetData(bt4, 4);
MakeLeftSubTree(bt1, bt2);
MakeRightSubTree(bt1, bt3);
MakeLeftSubTree(bt2, bt4);
printf("%d \n",
GetData(GetLeftSubTree(bt1)));
printf("%d \n",
GetData(GetLeftSubTree(GetLeftSubTree(bt1))));
return 0;
}
둘 이상의 노드로 이뤄져 있는 서브 트리를 완전히 삭제하려면 서브 트리를 구성하는 모든 노드를 대상으로 free 함수를 호출해야 한다.
순회 : 모든 노드를 방문하는 것
전위 순회(Preorder Traversal) : 루트 노드를 먼저
중위 순회(Inorder Traversal) : 루트 노드를 중간에
후위 순회(Postorder Traversal) : 루트 노드를 마지막에
ex)
BinaryTreeTraverseMain.c
#include <stdio.h>
#include "BinaryTree.h"
void InorderTraverse(BTreeNode * bt)
{
if(bt == NULL) // bt가 NULL이면 재귀 탈출!
return;
InorderTraverse(bt->left);
printf("%d \n", bt->data);
InorderTraverse(bt->right);
}
int main(void)
{
BTreeNode * bt1 = MakeBTreeNode();
BTreeNode * bt2 = MakeBTreeNode();
BTreeNode * bt3 = MakeBTreeNode();
BTreeNode * bt4 = MakeBTreeNode();
SetData(bt1, 1);
SetData(bt2, 2);
SetData(bt3, 3);
SetData(bt4, 4);
MakeLeftSubTree(bt1, bt2);
MakeRightSubTree(bt1, bt3);
MakeLeftSubTree(bt2, bt4);
InorderTraverse(bt1);
return 0;
}
'책 > 윤성우의 열혈 자료구조' 카테고리의 다른 글
| 정렬(sorting) (0) | 2020.10.28 |
|---|---|
| 우선순위 큐와 힙 (0) | 2020.10.25 |
| 큐(Queue) (0) | 2020.10.22 |
| 스택(Stack) (0) | 2020.10.22 |
| 연결 리스트(Linked List)3 (0) | 2020.10.19 |
