티스토리 뷰
그래프의 이해와 종류
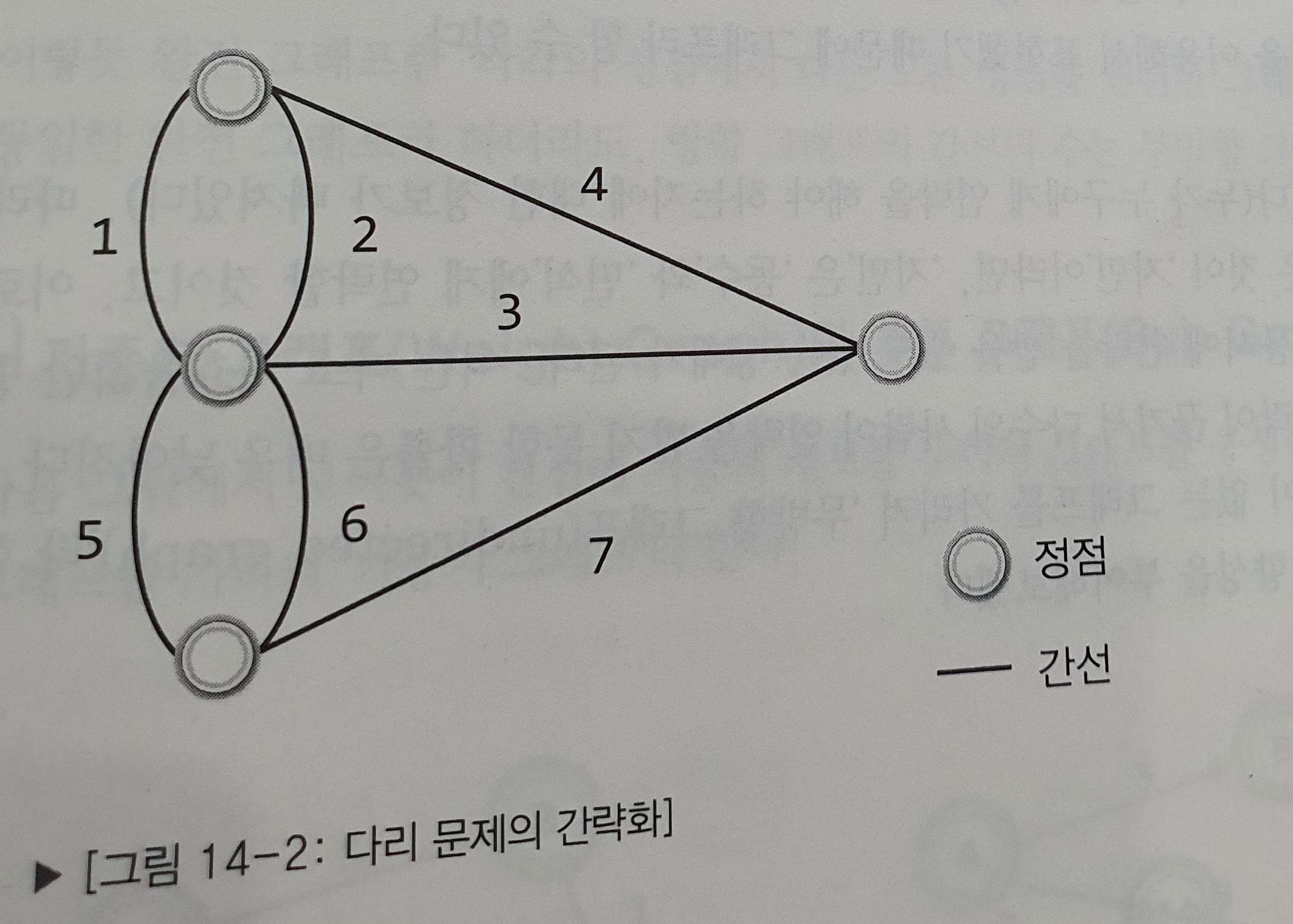
쾨니히스베르크의 다리 문제
모든 다리를 한번씩만 건너서 처음 출발한 장소로 돌아올 수 있는가?
정점 별로 연결된 간선의 수가 모두 짝수여야, 간선을 한번씩만 지나서 처음 출발했던 정점으로 돌아올 수 있다.
무방향 그래프 : 방향성 x
방향 그래프 : 방향성 o
완전 그래프 : 각각의 정점에서 다른 모든 정점을 연결한 그래프
가중치 그래프 : 간선에 가중치 정보를 두어서 그래프를 구성(이동시간)
부분 그래프 : 원 그래프의 일부 정점 및 간선으로 이뤄진 그래프를 뜻한다.
그래프의 집합 표현
그래프 G의 정점 집합 : V(G)={A,B,C,D}
그래프 G의 간선 집합
무방향 E(G)={(A,B),(A,C),(A,D)}
방향 E(g)={<A,B>,<A,C>,<A,D>}
그래프를 구현하는 두 가지 방법
인접 행렬 기반 그래프 : 정방 행렬을 활용(2차원 배열)
인접 리스트 기반 그래프 : 연결 리스트를 활용
인접 리스트 기반의 그래프 구현
ex)
ALGraph.h
#ifndef __AL_GRAPH__
#define __AL_GRAPH__
#include "DLinkedList.h"
// 정점의 이름들을 상수화
enum {A, B, C, D, E, F, G, H, I, J};
typedef struct _ual
{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
} ALGraph;
// 그래프의 초기화
void GraphInit(ALGraph * pg, int nv);
// 그래프의 리소스 해제
void GraphDestroy(ALGraph * pg);
// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV);
// 유틸리티 함수: 간선의 정보 출력
void ShowGraphEdgeInfo(ALGraph * pg);
#endifALGraph.c
#include <stdio.h>
#include <stdlib.h>
#include "ALGraph.h"
#include "DLinkedList.h"
int WhoIsPrecede(int data1, int data2);
// 그래프의 초기화
void GraphInit(ALGraph * pg, int nv)
{
int i;
pg->adjList = (List*)malloc(sizeof(List)*nv);
pg->numV = nv;
pg->numE = 0; // 초기의 간선 수는 0개
for(i=0; i<nv; i++)
{
ListInit(&(pg->adjList[i]));
SetSortRule(&(pg->adjList[i]), WhoIsPrecede);
}
}
// 그래프 리소스의 해제
void GraphDestroy(ALGraph * pg)
{
if(pg->adjList != NULL)
free(pg->adjList);
}
// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE += 1;
}
// 유틸리티 함수: 간선의 정보 출력
void ShowGraphEdgeInfo(ALGraph * pg)
{
int i;
int vx;
for(i=0; i<pg->numV; i++)
{
printf("%c와 연결된 정점: ", i + 65);
if(LFirst(&(pg->adjList[i]), &vx))
{
printf("%c ", vx + 65);
while(LNext(&(pg->adjList[i]), &vx))
printf("%c ", vx + 65);
}
printf("\n");
}
}
int WhoIsPrecede(int data1, int data2)
{
if(data1 < data2)
return 0;
else
return 1;
}
ALGraphMain.c
#include <stdio.h>
#include "ALGraph.h"
int main(void)
{
ALGraph graph;
GraphInit(&graph, 5); // A, B, C, D, E의 정점 생성
AddEdge(&graph, A, B);
AddEdge(&graph, A, D);
AddEdge(&graph, B, C);
AddEdge(&graph, C, D);
AddEdge(&graph, D, E);
AddEdge(&graph, E, A);
ShowGraphEdgeInfo(&graph);
GraphDestroy(&graph);
return 0;
}DLinkedList 생략
그래프의 탐색
그래프의 탐색은 복잡하다.
깊이 우선 탐색(Depth First Search:DFS)
한 사람에게 연락을 취하는 방식(비밀)

ex) 비상연락망
1. 한 사람에게만 연락을 한다.
2. 연락할 사람이 없으면, 자신에게 연락한 사람에게 이를 알린다.
3. 처음 연락을 시작한 사람의 위치에서 연락은 끝이 난다.
스택 : 경로 정보의 추적을 목적으로 한다.
배열 : 방문 정보의 기록을 목적으로 한다.
DFS에서는 갔던 길을 되돌아 오는 상황이 존재. 이 때 필요한 것이 스택
동수를 떠나서 지민에게 방문할 때, 떠나는 동수의 이름을(정보를) 스택으로 옮긴다.
수정의 차례인데, 수정과 연결된 사람들이 모두 연락을 받았으니 자신에게 연락한 사람에게 연락의 기회를 넘긴다.
그게 스택의 맨 위에 쌓인 사람의 이름이다. POP
돌아갈 때는 스택에서 pop을 하면서 돌아가면 된다.
너비 우선 탐색(Breadth First Search : BFS)
자신에게 연결된 모든 사람에게 연락을 취하는 방식(소문)

큐 : 방문 차례의 기록을 목적으로 한다.
배열 : 방문 정보의 기록을 목적으로 한다.
연락을 받은 동수, 민석이 큐에 들어간다.
dequeue하면 동수가 나오고 동수를 기준으로 연락을 취해 지민을 enqueue한다.
dequeue하면 민석이 나오고 민석을 기준으로 연락을 취해 수정 정희를 enqueue한다.
dequeue하면 지민이 나오고 지민을 기준으로 연락을 취할 대상이 없으니 넘어간다.
dequeue하면 수정이 나오고 수정을 기준으로 연락을 취할 대상이 없으니 넘어간다.
dequeue하면 정희가 나오고 정희을 기준으로 연락을 취해 영석을 enqueue한다.
최소 비용 신장 트리
사실 트리는 그래프의 한 유형이다.
경로 : 두 개의 정점을 잇는 간선을 순서대로 나열한 것
단순 경로(simple path) : 동일한 간선을 중복하여 포함하지 않는 경로
사이클 : 단순 경로이면서 시작과 끝이 같은 경로
신장 트리(spanning tree) : 사이클을 형성하지 않는 그래프
신장 트리의 특징
1. 그래프의 모든 정점이 간선에 의해서 하나로 연결되어 있다.
2. 그래프 내에서 사이클을 형성하지 않는다.
최소 비용 신장 트리(minimum cost spanning tree) : 신장 트리의 모든 간선의 가중치 합이 최소인 그래프
크루스칼 알고리즘1
크루스칼 알고리즘 : 가중치를 기준으로 간선을 정렬한 후에 MST가 될때까지 간선을 하나씩 선택 또는 삭제해 나가는 방식
가중치가 낮은 간선들을 하나씩 추가해보자. 그러다보면 사이클이 형성된다. 사이클을 만드는 간선은 그래프에 추가하지 않는다.
간선의 수+1=정점의 수
크루스칼 알고리즘 핵심
1. 가중치를 기준으로 간선을 오름차순으로 정렬한다.
2. 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가한다.
3. 사이클을 형성하는 간선은 추가하지 않는다.
4. 간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
프림 알고리즘 : 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식(넘어가~~)
크루스칼 알고리즘2
간선을 내림차순으로 정렬하면 낮은 가중치의 간선을 하나씩 추가하는 방식이 아니라, 높은 가중치의 간선을 하나씩 빼는 방식으로 알고리즘이 전개된다.
두 정점이 다른 경로를 통해서도 연결되어 있는 경우에만 해당 간선을 삭제할 수 있다.
핵심
1. 가중치를 기준으로 간선을 내림차순으로 정렬한다.
2. 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거한다.
3. 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않는다.
4. 간선의 수가 정점의 수보다 하나 적을 때 MST는 완성된다.
'책 > 윤성우의 열혈 자료구조' 카테고리의 다른 글
| 테이블(Table)과 해쉬(Hash) (0) | 2020.10.31 |
|---|---|
| 탐색(Search) 2 (0) | 2020.10.31 |
| 탐색(Search) 1 (0) | 2020.10.30 |
| 정렬(sorting) (0) | 2020.10.28 |
| 우선순위 큐와 힙 (0) | 2020.10.25 |

